
Razones Trigonométricas de Ángulos de 45°, 30° y 60° para Segundo de Secundaria Fichas GRATIS
#julioprofe demuestra cómo obtener los valores exactos de seno, coseno, tangente, secante, cosecante y cotangente para los ángulos de 30°, 45° y 60°.Tema: #R.

RAZONES Trigonométricas de 30, 45 y 60 🔵 CIRCUNFERENCIA Goniométrica YouTube
Para determinar las razones trigonométricas de un ángulo de 45º (o su equivalente π/4 rad) tomaremos un cuadrado de lado l y lo dividiremos por su diagonal provocando que aparezcan dos triángulos isósceles. Recuerda que un triángulo isósceles tiene dos ángulos de 45º y uno de 90º. Descomposición de un cuadrado

Razones trigonométricas de 45°, 60° y 30° YouTube
Aprendemos a calcular las Razones Trigonométricas de los Ángulos Notables: 30º, 45º y 60º, concretamente el seno, el coseno y la tangente. Lo hacemos SIN cal.

Funciones Trigonométricas para los Ángulos Notables 30 y 60 grados YouTube
www.matematicasyeso.es ----- Sigue los vídeos en orden desde esta web En este vídeo vamos a ver las razones trigonométricas de 30°, 45° y 60°.
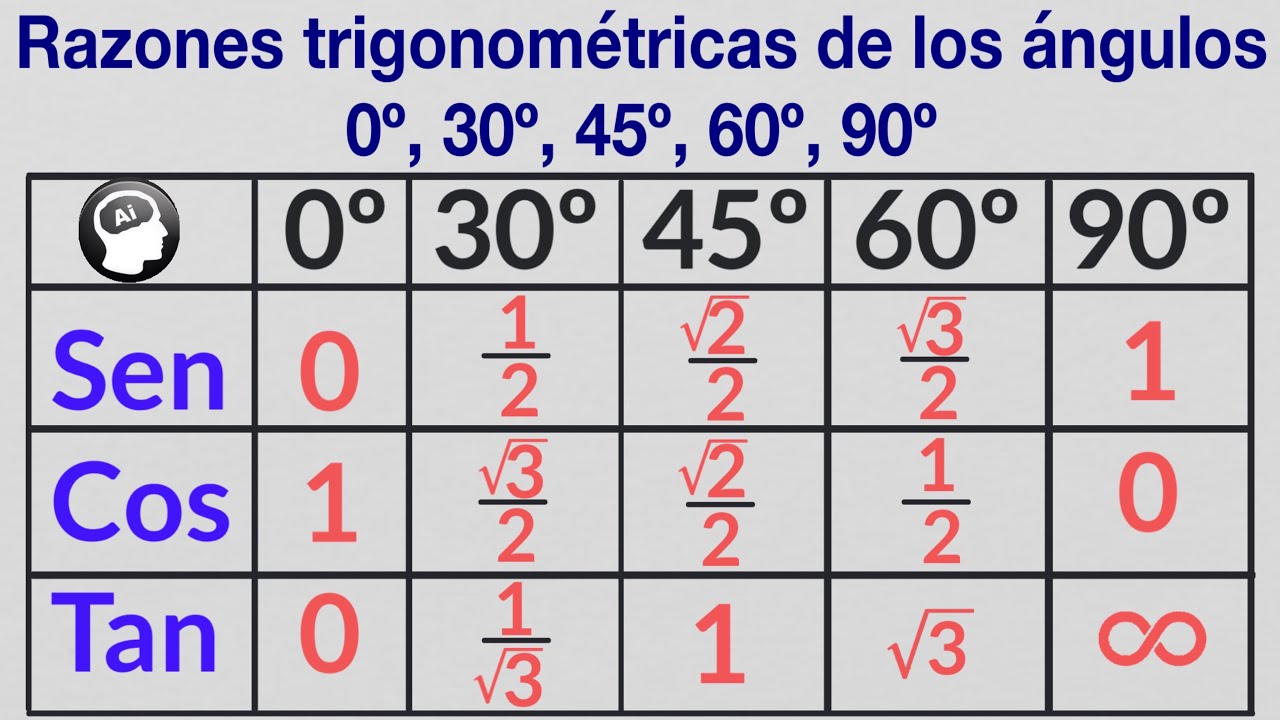
Razones trigonometricas de los angulos 0° 30° 45° 60° y 90° YouTube
1. babilonicos 2. griegos 3. isaacnewton 4. euler 5. leibnis 6. astronomos 7. indues. Ver todas las clases. Presenta TOMi.digital - RAZONES TRIGONOMETRICAS DE LOS ANGULOS DE 30, 45 Y 60 GRADO en clase, aumenta la participación de tus estudiantes con divertidas actividades a la vez que repasan conceptos.

RAZONES TRIGONOMÉTRICAS de 30, 45 y 60 🕐 📐🕑 YouTube
Calcula el valor de: sin 2 30 ° + cos 2 45 ° + tan 2 60 ° sin 2 60 ° + cos 2 30 ° + tan 2 45 ° Resolvemos la situación En primer lugar vamos a reemplazar las razones trigonométricas de los ángulos notables.
.gif)
ÁNGULOS AGUDOS DE 30º Y 60° SENO COSENO TANGENTE COTANGENTE SECANTE COSECANTE EJEMPLOS RESUELTOS
Razones trigonométricas de 30º, 45º y 60º. Regla nemotécnica para calcular los ángulos notables. Ejemplos resueltos. E.S.O. Bachillerato Álgebra Cálculo Funciones Geometría Trigonometría Gometría Analítica Derivadas Integrales Estadística INICIO Álgebra Geometría Trigonometría Geom. Analítica Cálculo Estadística E.S.O. 1º E.S.O. 2º E.S.O. 3º E.S.O.
.png)
TRIÁNGULOS DE 45° Y 45° 30° Y 60° 37° Y 53° 16° Y 74° EJERCICIOS RESUELTOS DE RAZONES
Razones trigonométricas del ángulo de 45º Razones trigonométricas del ángulo de 60° Para hallar las razones del ángulo de 60° debemos partir de un triángulo rectángulo con un ángulo agudo de esa medida. Podemos construir un triángulo así de una forma muy sencilla de recordar.
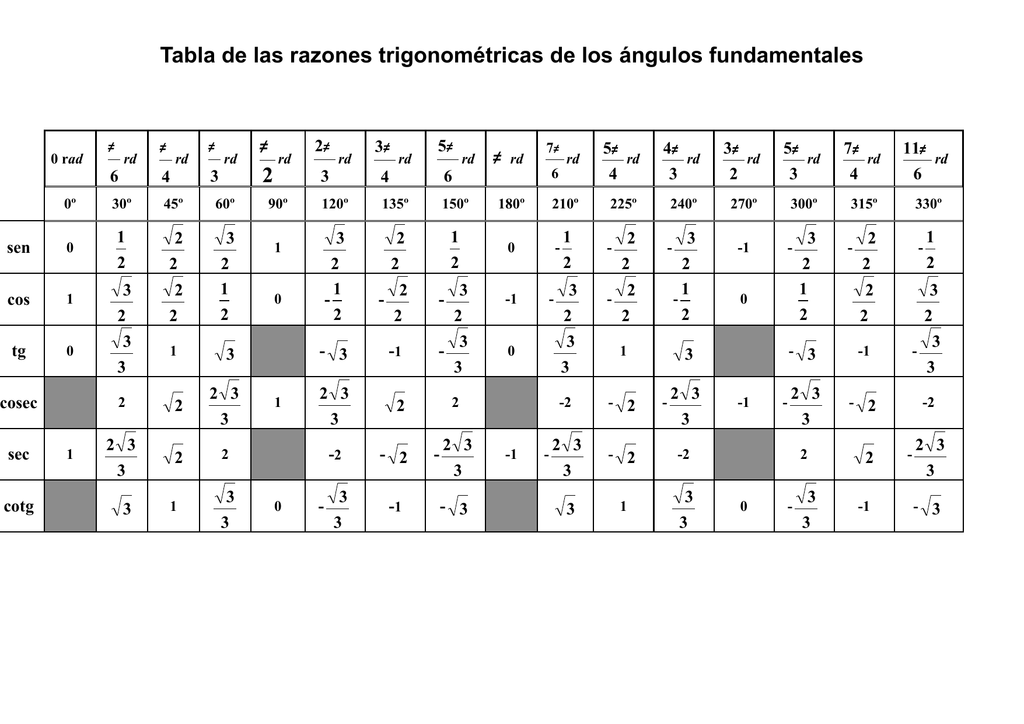
tutam Fırın Çarşamba tabla trigonometrica
Utilizaremos expresiones de raíz cuadrada cuando usemos el teorema de Pitágoras para obtener una longitud lateral. Las razones trigonométricas para ángulos de referencia, como 30 ° , 45 ° y 60 ° , dependen de expresiones con raíz cuadrada.

Razones Trigonometricas De Angulos Notables De 30 60 45 37 Y 53 Exactos Y Aproximados Theme Loader
As razões trigonométricas de 30º, 45º e 60º Considere as figuras: Quadrado de lado l e diagonal Triângulo equilátero de lado I e altura Seno, cosseno e tangente de 30º Aplicando as definições de seno, cosseno e tangente para os ângulos de 30º, temos: Seno, cosseno e tangente de 45º

Razones trigonometricas de 0, 30, 45, 60, 90, 180, 270 y 360º SECUNDARIA (4ºESO) matematicas
RAZONES TRIGONOMÉTRICAS de 30, 45 y 60 🕐 📐🕑 ¡Ángulos, ángulos, ángulos por todas partes! Queremos medir entender estos objetos tan importantes para un sinfín de disciplinas como: arquitectura, ingeniería, astronomía o matemáticas. Por cierto hasta en los emojis de whatsapp aparecen

RAZONES TRIGONOMÉTRICAS DE 30°, 45° Y 60° (DEMOSTRACIÓN) YouTube
Razones trigonométricas de ángulos notables En este artículo obtendremos los valores exactos de las funciones trigonométricas seno, coseno y tangente para los ángulos de 30°, 45° y 60°. Estos ángulos forman parte, junto con los ángulos de 0° y 90°, de los bien conocidos ángulos notables.
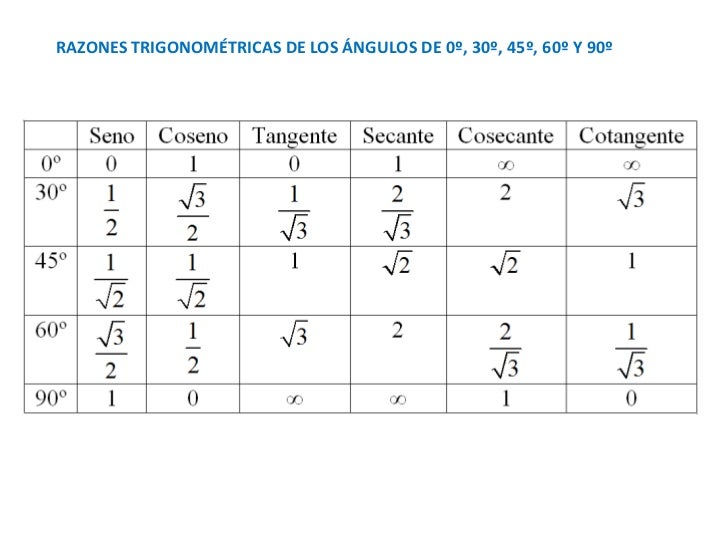
[Maths] 3.3 trigonometria
VDOMDHTMLtml> Razones Trigonométricas de 30 45 60 (Obtención de valores exactos) - YouTube Los 3 ángulos más utilizados en cualquier estructura hecha por el hombre son los de 30º,.
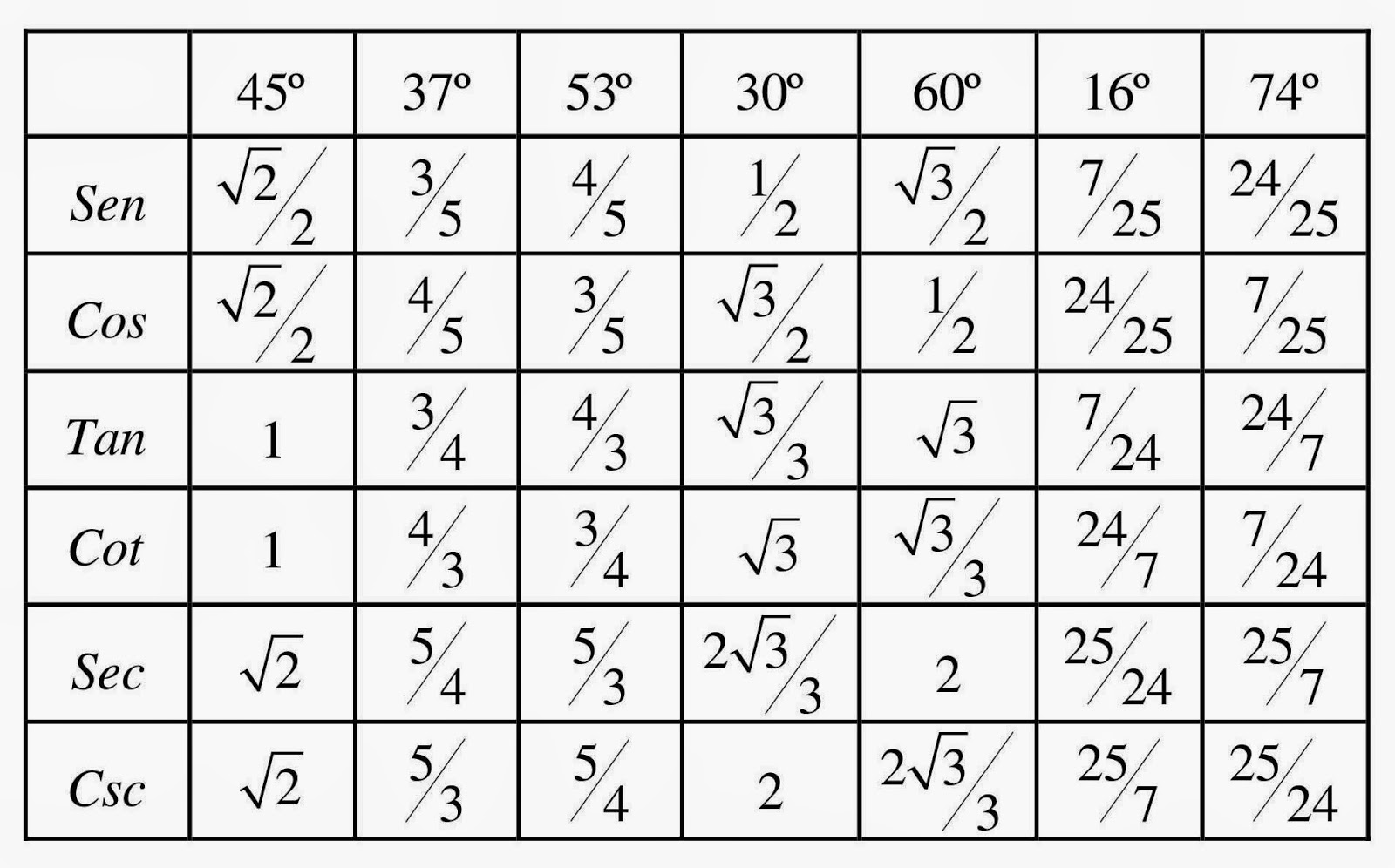
Tabela Trigonométrica 0 A 360 AskSchool
Un triángulo 45-45-90 es un triángulo rectángulo con dos ángulos de 45 ∘ . La hipotenusa es raíz cuadrada de 2 veces más grande que cualquiera de los lados. 45 ∘ 45 ∘ x x x 2 [Yo soy escéptico. ¿Me pueden mostrar cómo determinar estas razones?] Las razones trigonométricas de 30 ∘

RAZONES TRIGONOMÉTRICAS DE 30°, 45° Y 60°. HD YouTube
RAZONES TRIGONOMÉTRICAS de 30, 45 y 60 🕐 📐🕑 Archimedes Tube 75.3K subscribers 354 14K views 4 years ago ¡Aquí esta nuestra tercera entrega sobre trigonometría! En este capítulo.

Razones trigonométricas para ángulos de 30 45 y 60 grados FÁCIL YouTube
Las razones trigonométricas para el ángulo α=60^ {\circ} α = 60∘ se pueden obtener utilizando el teorema de Pitágoras y el hecho de que dicho ángulo aparece de manera natural en los triángulos equiláteros. Supón que se tiene un triángulo equilátero cuyos tres lados miden 1 1.